光弹法检测
真空玻璃真空度是实验应力分析中的一种基本方法,是基于力学基础之上的,在介绍该方法前,首先对真空玻璃内部应力分布状态作简单的分析。
1、真空玻璃支撑应力分析
双层真空玻璃在外部大气压作用下,将产生很大的应力和变形。为保证玻璃不因大气压而产生过大的应力,在真空玻璃内部放置许多金属支撑物如图1所示,玻璃与支撑物相互作用抵消了玻璃内外大气压差带来的附加外力。显然,当大气压差越大时,支撑物与玻璃的相互作用力越大,而且支撑力的大小与气压差成线性比例关系。为分析真空玻璃支撑点处的应力分布特征,根据真空玻璃结构特点,可以将真空玻璃每点支撑区域划分为一个单元进行受力分析,其一个单元的受力力学理论计算模型可简化为图2所示。
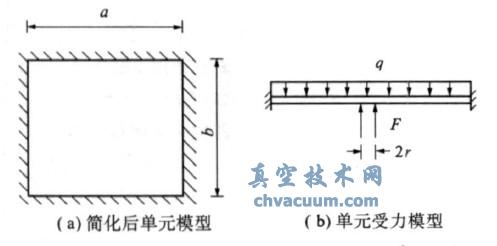
图2 真空玻璃的支撑应力模型图
单元模型可认为是四边固支,在均布压力q及支撑力F 的作用下,最大应力将出现在玻璃与支撑物支撑点处,计算公式计算如下:

式中:a,b 分别为真空玻璃支撑点的横向和纵向距离;F = qab;t为单片玻璃厚度;r 为支撑物半径;A、B、B1 分别为系数,当a /b= 1时,A= 0.0138,B= 0.1386,B1 = 0.1386。
根据上述计算公式,支撑点位置处产生的最大应力与真空玻璃支撑物排列距离、方式、支撑物大小,真空玻璃单片玻璃厚度及真空度有关。显然,当真空玻璃结构确定时,支撑处的最大应力应与玻璃的内外压差成正比。
根据上面的理论计算方法,笔者对一真空玻璃样品进行了计算,并同时对其进行了有限元分析,真空玻璃为钠钙普通玻璃,E = 72 GPa,v =0.22,玻璃单片厚度为4 mm,支撑物为不锈钢,直径为0.4 mm,支撑物长宽间距分别为3 cm. 根据上面的理论公式进行了计算,计算结果为Rmax=11.057 MPa,有限元分析结果得到Rmax =11.9MPa,两者误差相差7.62%,有限元得到的等效应力分布图见图3。由上面的计算及分析结果表明,支点处会产生应力集中,该处应力最大,由玻璃内外压差而带来的附加力基本上呈均匀状态分布于真空玻璃内部的各个支点上,各支点处的最大应力均在玻璃设计强度允许范围内。

图3 ANSYS模拟真空玻璃支撑等效应力云图
2、光弹法检测真空度的基本原理
根据上面对真空玻璃应力分析,我们知道在真空玻璃支撑物与玻璃支撑位置处会产生应力集中,该位置玻璃应力最大。而且最大应力与玻璃的真空度有关,当玻璃真空度完全损失时,它们之间的作用力也完全消失。根据光弹性原理,材料在外力作用下会产生临时双折射现象,而这种现象是可以通过光弹仪观测得到的。图4为通过光弹仪观测到一单片玻璃厚为4mm,支撑点间距为3 cm的双层真空玻璃的应力光斑,光斑为梅花形状,应力光斑的形状与大小与该处的主应力值有关。

图4 通过光弹仪观测到真空玻璃应力光斑图
我们知道,在支撑物与玻璃相互接触位置点处为三向应力状态,在该接触点取一微小单元体,在支撑物与玻璃的接触面上,有接触应力R3,由于R3 的作用,单元体将向周围膨胀,于是引起周围玻璃对它的约束应力R1 和R2。由于实际支撑物结构尺寸很小,因此,支撑点处可以把支撑力看作为集中荷载,玻璃看作半无限大平面体。


